Style 배분 전략

Jul 13, 2024

S&P U.S. Style Indices Methodology

예전에 ‘포트폴리오 구축’을 주제로 팀프로젝트를 한 적이 있는데, 그 때 S&P U.S. Style Indices Methodology 문서를 참고하여 파이썬으로 가치/성장 스타일 투자를 구현한 경험이 있다.
이 방법론의 핵심은

모든 종목에는 가치주의 성격과 성장주의 성격이 혼합되어 있고, 둘 중 어느 쪽에 더 치우쳐져있는지를 가치점수(Value Score) 와 성장점수(Growth Score)판단하겠다는 아이디어

라고 보면 된다.

소스코드 :

| 프로젝트 Repo :

성장이 뭐죠? 가치는요?

성장주의 핵심은 미래의 성장 가능성을 높게 평가하고, 주가 상승을 통해 수익을 실현하는 것

가치주의 핵심은 시장의 일시적인 왜곡이나 기업의 잠재력이 반영되지 않는 저평가된 주식을 찾아내어, 주가가 본래의 가치로 회귀할 때 까지 보유함으로써 수익을 실현하는 것

이렇게 대답하는게 가장 깔끔해 보인다. 😤

네이버증권 주식 정보를 호출하는 pykrx 라이브러리를 활용하여 직접 코스피 종목의 스타일 점수를 측정해보자!

위에서 설명했듯이, 주식의 가치주적 요소와 성장주적인 요소를 점수로 평가 해야하므로 이를 위한 가치 평가 지표, 성장 평가 지표가 있어야 한다.
아래는 문서에서 제시한 지표이다. 해당 지표를 pykrx로 계산해보았다. 계산 시점은 임의로 6월 첫번째 장날로 지정하였다.
모든 지표 계산에 공통적으로 두 가지 전처리 방법이 들어가는데,

winsorize : 데이터의 이상치를 처리하는 방법으로 상한 하한을 각 양끝의 0.05 로 설정하는 방법이다. 즉, 전체 범위의 0.05 ~ 0.95 에만 데이터가 존재하게 하는 방법이다. 이 방법을 쓰면 이상치 데이터를 제거하지 않아도 된다. 실제 금융데이터의 이상치 처리에서 많이 쓰이는 기법이라고 한다.
z정규화 : 각 수치들의 범위가 다 다르기 때문에 객관적인 비교를 위해 정규화를 진행한다.

Growth Factors

Three-Year Net Change in Earnings per Share(Excluding Extra Items) over Current Price
최근 3년 동안의 주당 순이익(EPS)의 변화를 현재 주가와 비교하는 것이다.
해당 지표 값이 높을수록 회사의 성장 잠재력이 높다고 평가할 수 있다.
피터린치가 만든 PEG의 역수이다.

# 3년 EPS 증가율 구하기
df_21 = pd.DataFrame(stock.get_market_fundamental('2021-06-01',market="KOSPI")['EPS'])
df_21.rename(columns={'EPS':'EPS_21'},inplace=True)
df_24 = pd.DataFrame(stock.get_market_fundamental('2024-06-03',market="KOSPI")['EPS'])
df_24.rename(columns={'EPS':'EPS_24'},inplace=True)
eps = pd.merge(df_21,df_24,left_index=True,right_index=True,how='inner')
eps['NetChange'] = eps['EPS_24']-eps['EPS_21']

# 3년 EPS 증가율 대비 주가 (대략 PEG 개념)
eps = pd.merge(eps,close24,left_index=True,right_index=True,how='inner')
eps['approxPEG'] = (eps['NetChange']/eps['24'])
eps['win_P'] = winsorize(eps['approxPEG'],limits=[0.05,0.05])
eps.loc[eps['NetChange']==0,'win_P'] = 0 # 정규화하기 전에 필요
eps['stn_P'] = ss.zscore(eps['win_P'])

Momentum (12 Months % Price Change)
최근 12개월 동안의 주가 변동률을 나타낸다. 투자자들이 주식의 최근 성과를 평가할 때 주로 사용하며 높은 모멘텀은 주가가 상승 추세에 있음을 보여준다.

# 상장된 기업의 종가만 사용
close24 = pd.DataFrame({'24':stock.get_market_ohlcv('20240603',market="KOSPI")['종가']})
close21 = pd.DataFrame({'23':stock.get_market_ohlcv('20230601',market="KOSPI")['종가']})
ks = pd.merge(close21,close24,left_index=True,right_index=True,how='inner')

# 모멘텀 계산  
ks['Momentum'] =((ks['24']-ks['23'])/ks['23'])*100
ks.rename(columns={'23':'매수가','24':'매도가'},inplace=True)
ks['win_MM'] = winsorize(ks['Momentum'],limits=[0.05,0.05])
ks['stn_MM'] = ss.zscore(ks['win_MM'])

Three-Year Sales per Share Growth Rate 최근 3년 동안의 주당 매출 성장률을 의미한다.
회사의 매출이 주당 기준으로 얼마나 증가했는지 판단할 수 있으며, 해당 값이 높을수록 회사가 빠르게 성장하고 있음을 시사한다.

아쉽게도 pykrx에는 매출액 정보가 없어서 이 기준은 빼고 진행했다. 나중에 OpenDart나 직접 크롤링을 구현하여 추가할 수 있을 것 같다.

Growth Result

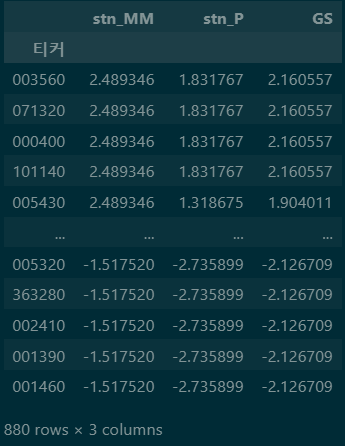
# 성장점수(GS) 만들기
growth_S = pd.merge(ks['stn_MM'],eps['stn_P'],left_index=True,right_index=True,how='inner')
growth_S['GS'] = (growth_S.iloc[:,0] + growth_S.iloc[:,1])/2
growth_S.sort_values('GS',ascending=False)

모멘텀과 EPS/P을 평균내어 최종 GS(Growth Score) 을 계산한다.

Value Factors

먼저 PER과 PBR의 역수를 구하고 시작하겠다. 역수를 구하는 이유는, PER과 PBR의 경우 그 값이 작을수록 저평가되었다고 판단하기 때문에 역수를 취함으로써 점수처럼 값이 커질 수록 저평가되었음을 판단하기 위해서이다.

fm = stock.get_market_fundamental('20240603',market="KOSPI")
fm['E/P'] = (1/fm['PER']) # 역수 취하기
fm['B/P'] = (1/fm['PBR'])
fm = fm.query('PER != 0').sort_values('PER') # 결측값 제거

Book Value to Price Ratio
회사의 장부 가치(Book Value)를 현재 주가로 나눈 비율이다. 이때 장부 가치는 회사의 순자산(자산-부채)으로 계산되며, 이 비율이 높을수록 주식이 저평가 되어있을 가능성이 높다.
PBR의 역수이다.
```
# B/P 구하기
bp  = pd.DataFrame({'B/P':fm['B/P'].sort_values(ascending=False)})
bp['winB/P'] = winsorize(bp['B/P'],limits=[0.05,0.05])
bp['stB/P'] = ss.zscore(bp['winB/P'])
```
Earnings To Price Ratio
회사의 주당 순이익(EPS)을 현재 주가로 나눈 비율이다.
주가 대비 순이익 비율(P/E 비율의 역수)로 이 비율이 높을수록 주식이 저평가 되었음을 의미한다.
PER의 역수이다.
```
# E/P 구하기
ep = pd.DataFrame({'E/P':fm['E/P'].sort_values(ascending=False)})
ep['winE/P'] = winsorize(ep['E/P'],limits=[0.05,0.05])  # 이상치 조절
ep['stE/P'] = ss.zscore(ep['winE/P']) # z-score
```
Sales to Price Ratio
회사의 주당 매출을 현재 주가로 나눈 비율이다. 주가 대비 매출 비율로, 이 비율이 높을수록 주식이 저평가되었을 가능성이 있다.

이 지표도 마찬가지로 pykrx에 매출 정보가 없기 때문에 이번 작업에서는 제외하겠다.

Value Result

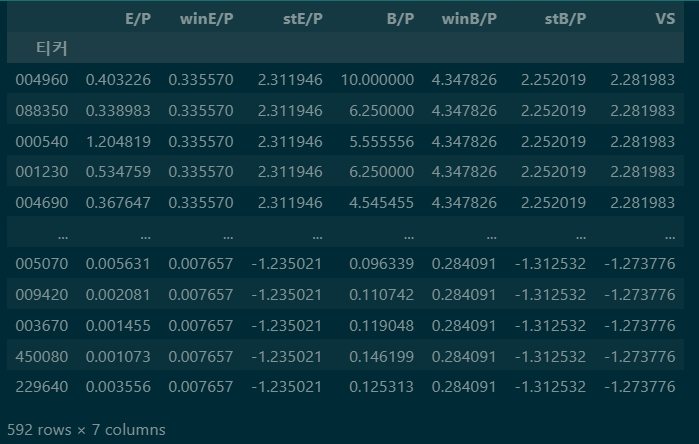
# 가치점수(VS) 만들기
value_S = pd.merge(ep,bp,left_index=True,right_index=True,how='inner')
value_S['VS'] = (value_S.iloc[:,2]+value_S.iloc[:,5])/2
value_S.sort_values(by='VS',ascending=False)

가치점수인 VS(Value Score)도 E/P 와 B/P 의 평균으로 구해준다.

최종 순위 구하기

이렇게 코스피 각 종목의 가치점수와 성장점수를 부여해봤다. 이제 그럼 이제 성장과 가치로 분류를 하면 된다.
순서는 다음과 같다.

종목별로 GS Rank 와 VS Rank 를 계산한다. 순위매기는 거라고 생각하면 된다.

# 데이터 합치기
style = pd.merge(value_S['VS'],growth_S['GS'],left_index=True,right_index=True,how='inner')
style= style.sort_values('GS',ascending=False)

# 성장 점수 순위 컬럼 생성
style['GS_Rank'] = style['GS'].rank(method='min',ascending=False)

# 가치 점수 순위 컬럼 생성
style['VS_Rank'] = style['VS'].rank(method='min',ascending=False)

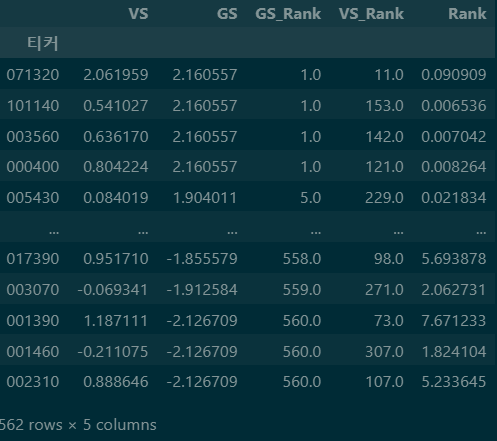
GS_Rank / VS_Rank 를 계산하여 정렬한다. 이 값을 기준으로 최종 순위를 매긴다.

# 스타일 순위 매기기 
style['Rank'] = style['GS_Rank']/style['VS_Rank']

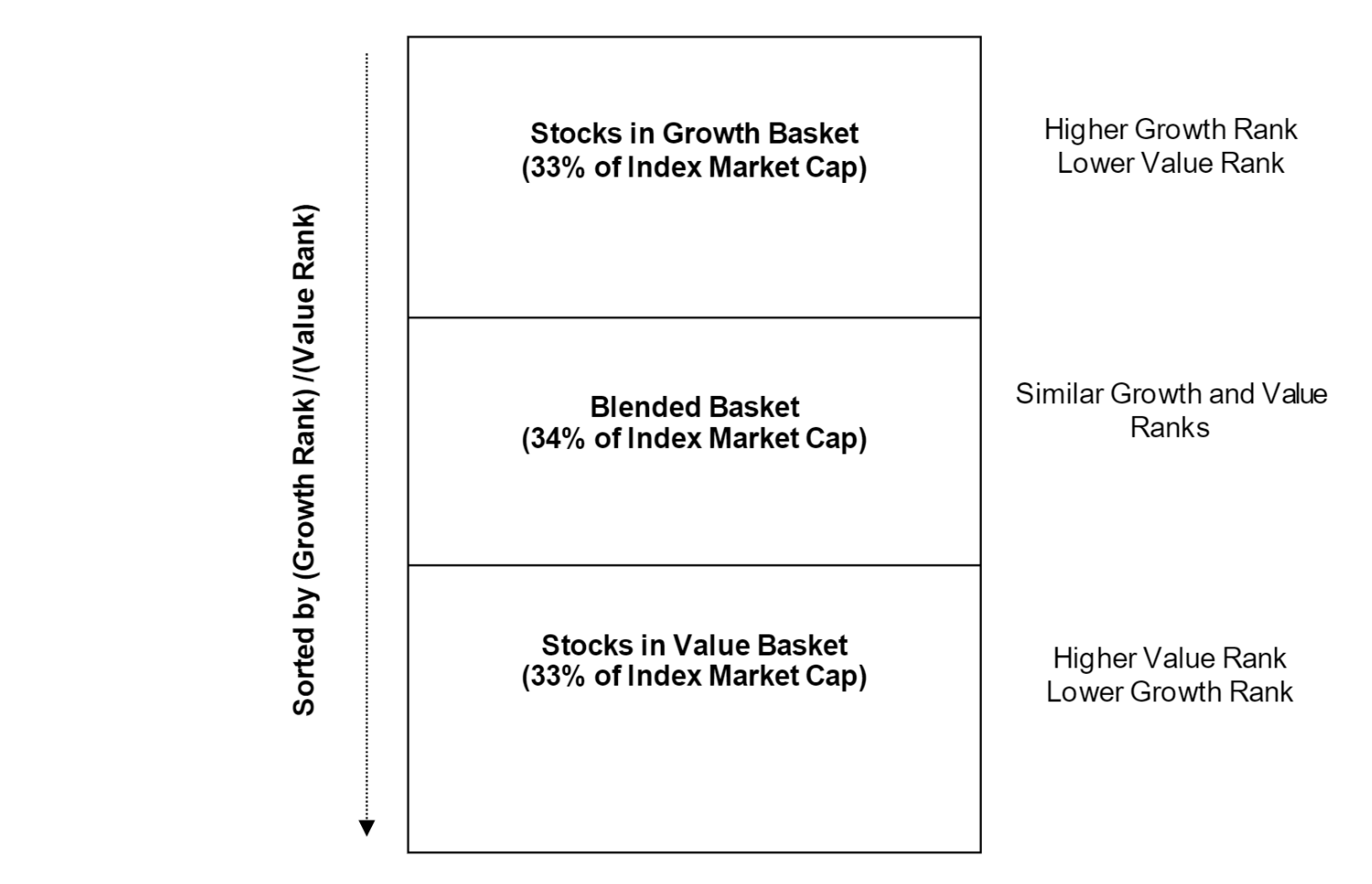
시가총액을 기준으로 그룹을 Growth, Neutral, Value로 구분한다.

# 시가총액 불러오기
cap = pd.DataFrame(stock.get_market_cap('20240603',market="KOSPI")['시가총액'])
style_dt= pd.merge(style,cap,left_index=True,right_index=True,how='inner')
total_cap = style_dt.시가총액.sum()

# 전체 시총 대비 개별 종목 시총 비율 구하기
style_dt['cap_ratio'] = style_dt.iloc[:,5]/total_cap

# 개별 종목 시총 누적비율 컬럼 생성
style_dt=style_dt.sort_values(by='Rank')
style_dt['cum_cap'] = style_dt['cap_ratio'].cumsum()

# 시총 비율로 3구간 나눠서 성장,중간,가치 그룹화 하기
GS = style_dt[style_dt['cum_cap'] <= 0.33]
GS['group'] = 'growth'

NEUTRAL = style_dt[(style_dt['cum_cap'] > 0.33) & (style_dt['cum_cap'] <= 0.67)]
NEUTRAL['group'] = 'neutral'

VS = style_dt[style_dt['cum_cap']>0.67]
VS['group'] = 'value'

style_group = pd.concat([GS,NEUTRAL,VS],axis=0)

먼저 코스피의 종목 중 style 그룹에 속해있는 종목들만 뽑아서 시가총액 합을 구해준다.
그리고 각 종목의 시가총액 비율을 누적합으로 구한 다음 0~33, 33~67, 68~100 으로 세 구간을 나눠준다. 순서별로 성장그룹, 중립그룹, 가치그룹으로 분류해주면 된다.

결과를 확인해보면

# 나눈 구간으로 실제 시총 비율 확인하기 
growth_cap = style_group.groupby('group').get_group('growth').sum().시가총액
neutral_cap = style_group.groupby('group').get_group('neutral').sum().시가총액
value_cap = style_group.groupby('group').get_group('value').sum().시가총액

print((growth_cap/total_cap)*100)
print((neutral_cap/total_cap)*100)
print((value_cap/total_cap)*100)

# 스타일별 종목 개수 확인
print('\n',style_group.group.value_counts())
'''
31.633205801881942
35.36428009359327
33.002514104524785

 group
value      393
growth     153
neutral     16
'''

각 그룹의 비율은 적절하게 삼등분된 걸 알 수 있다. 그룹별 속한 종목의 수를 보면 가치 종목이 절반 이상이고, 중립그룹은 16개로 그 수가 적은 것을 알 수 있다. 22년도에 프로젝트 했을 때도 중립 그룹 수가 가장 적긴 했지만 그때는 76개로 지금보다 더 많았다. 원인을 찾아보니, 중립그룹에 속한 삼성전자가의 시가총액 비율이 무려 27%나 차지했다. 그러다 보니 자연스럽게 중립그룹의 종목 수가 적을 수밖에..

산점도로 각 그룹 종목 현황 파악하기

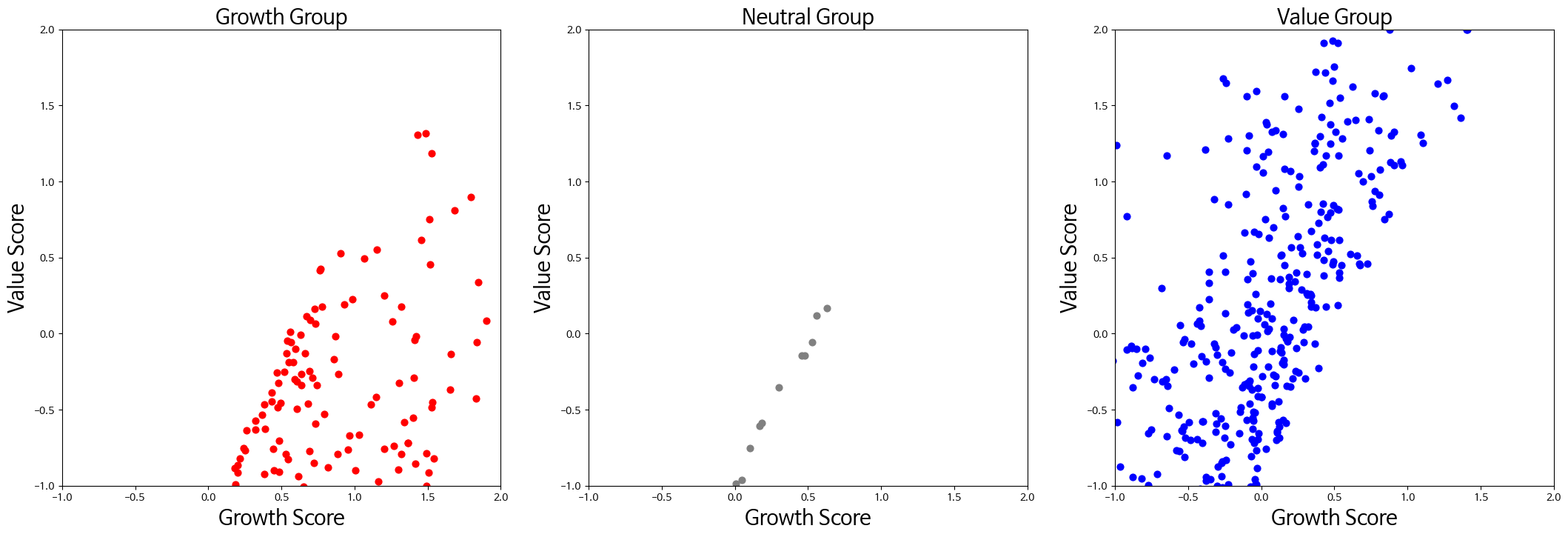
더 보기 편하게 plotly로 가져와봤다. (모바일 환경에서는 보기 불편할 수 있음)

위의 scatter 차트의 범례를 하나씩 클릭하면 각 그룹의 종목들만 볼 수 있다. (성장점수, 가치점수) , 종목코드 순으로 popup정보가 뜬다.

Neutral 그룹 분류하기

회색으로 표현된 종목들은 Neutral 이라고 해서 가치 요소와 성장 요소가 상대적으로 골고루 갖춰진 종목이라고 보면 된다.
이 중립그룹도 다시 가치그룹과 성장그룹으로 분류할 수가 있다. 중립 종목이 각 그룹에게서 떨어진 거리를 측정하는 아이디어이다.
이 부분의 내용은 문서의 Appendix I (p22)에 설명되어 있다.

그룹별 점수 평균 구하기

n = NEUTRAL # 향후 작업 편의를 위해 중립그룹을 n으로 지정
print(f'AV_G :{VS.GS.mean()}') # 가치그룹의 평균 성장점수
print(f'AV_V :{VS.VS.mean()}') # 가치그룹의 평균 가치점수
print(f'AG_G :{GS.GS.mean()}') # 성장그룹의 평균 성장점수
print(f'AG_V :{GS.VS.mean()}') # 성장그룹의 평균 가치점수

'''
AV_G :-0.09683188730398012
AV_V :0.2589608805872862
AG_G :0.9230853249666636
AG_V :-0.4840451009196985
'''

Midpoint Distance로 그룹 판단하기 성장 그룹을 먼저 보면

# 첫번째 조건(IF) : 중립 종목의 성장 점수 >= 성장그룹의 평균 성장점수 
g_first = n[n['GS']>=GS.GS.mean()] 
# 해당 종목의 MD : 중립종목의 가치점수 - 성장그룹의 평균 가치점수
g_first['D(G,X)'] = abs(g_first.iloc[:,0]-GS.VS.mean())

# 두번째 조건(Else IF) : 중립 종목의 가치 점수 <= -성장그룹의 평균 가치점수
g_second = n[n['VS']<= GS.VS.mean()]
# 해당 종목의 MD : 성장그룹의 평균 성장 점수 - 중립 종목의 성장점수
g_second['D(G,X)'] =abs(GS.GS.mean() - g_second.iloc[:,1])

# 세번쨰 조건(Else) : 위의 두 가지 조건에 포함되지 않는 종목
g_third = n.drop(index=(g_first.index.tolist() + g_second.index.tolist()))
# 해당 종목의 MD 
g_third['D(G,X)'] = (((g_third.iloc[:,0])-GS.VS.mean())**2 + (GS.GS.mean()-g_third.iloc[:,1])**2)**(1/2)

# If/Else if/ Else 결과 합치기 
ng_total = pd.concat([g_first,g_second,g_third],axis=0)
ng_total

중립종목들의 성장그룹과의 거리를 구한 결과이다. 마지막 컬럼의 D(G,X) 를 보면 되며, 종목 X의 성장그룹G 와의 거리 D 를 뜻한다.

동일한 방법으로 가치그룹과의 거리를 구해보면,

# IF 에 해당
v_first = n[n['VS'] >= VS.VS.mean()]
v_first['D(V,X)'] = abs(v_first.iloc[:,1]-(VS.GS.mean()))

# Else if 에 해당
v_second = n[n['GS'] <= VS.GS.mean()]
v_second['D(V,X)'] = abs(VS.VS.mean() - v_second.iloc[:,0])

# Else 에 해당
v_thrid = n.drop(index=(v_first.index.tolist() + v_second.index.tolist()))
v_thrid['D(V,X)'] = ((v_thrid.VS-VS.VS.mean())**2 + (VS.GS.mean()-v_thrid.GS)**2)**(1/2)

# IF/Else if/Else 합치기
nv_total = pd.concat([v_first,v_second,v_thrid],axis=0)
nv_total

마지막 컬럼 D(V,X) 로 결과를 확인할 수 있다.

가중치 W 구하기 이제 중립 종목의 성장그룹, 가치그룹과의 거리를 구했으니 어느 쪽으로 더 가까운지 가중치를 구해서 판단할 차례이다. 종목 X 에 대하여

W(V,X) : Percentage of Float Market Capitalization of Company X in Value Index
= D(G,X)/(D(G,X) + D(V,X))
W(G,X) : Percentage of Float Market Capitalization of Company X in Growth Index
= D(V,X)/(D(G,X) + D(V,X))
W(V,X) + W(G,X) = 1

로 정의한다.

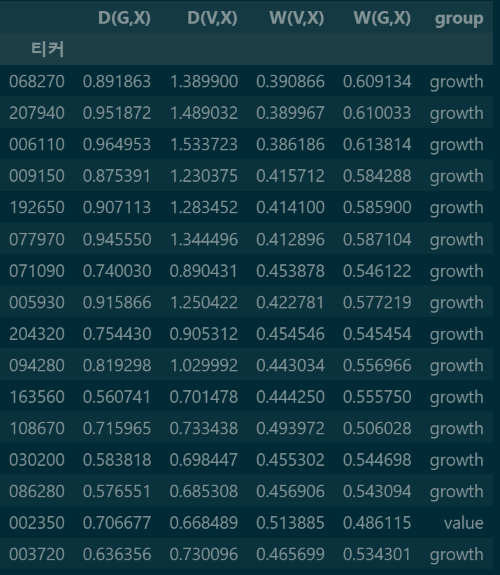
# ng,nv 데이터 합치기 
nw = pd.merge(ng_total['D(G,X)'],nv_total['D(V,X)'], left_index=True,right_index=True, how='inner')

# weight 구하기
nw['W(V,X)'] = nw['D(G,X)']/(nw['D(G,X)']+nw['D(V,X)'])
nw['W(G,X)'] = nw['D(V,X)']/(nw['D(G,X)']+nw['D(V,X)'])

이렇게 구한 다음 W(V,X) > W(G,X) 라면 Value 그룹, W(V,X) < W(G,X) 라면 Growth 그룹으로 분류한다.

티커 002350 만 가치그룹으로 분류되고 나머지는 전부 성장그룹으로 분류된 것을 알 수 있다. 삼성전자는 성장주로 분류된 것도 확인할 수 있다.

마무리…근데 마무리 아님.. 근데 이제 샤이니를 곁들인…

주가 정보는 매일 빠르게 변화하며 시장의 움직임을 보여주는 데이터이다. 이번 작업을 통해 금융시장의 움직임을 성장점수, 가치점수, 성장그룹, 가치그룹이라는 지표로 압축해 볼 수 있었다. 결국 지표라는 것은 대표성을 띄는 것이 중요하다고 생각한다. 지표명과 그 지표에 속해있는 요소들의 특성이 일치한다면 잘 만든 지표라고 할 수 있을 거다.
과거 프로젝트를 진행할 당시에도 이 같은 창의적인 접근이 매우 흥미로웠었기에 이번에 날짜와 그래프를 업데이트하여 다시 구현해보았다. 이번 게시글에서는 스타일 분류까지 진행했는데, 실제로 스타일 지수도 만들어볼 수 있다. 이 과정은 다음 게시글에서 다루기로 하겠다.

뜬금없긴 하지만 스타일 지수 작업을 하다보니 샤이니 덕질하던 때가 생각이 났다.
멤버 전원이 노래실력+춤실력+외모 조건을 충족한 샤이니…
샤이니라는 지표가 있고 멤버들이 그 안의 요소라고 생각하면 이건 절대 망하지 않는 투자이다. 🤭
실제로 나는 샤이니 데뷔 후 15년 동안 정말 행복한 덕질을 했고 여전히 덕질 이어가는 중이다.!!

다들 샤이니월드 했으면 좋겠다.

영원한 나의 우상, 동경하는 샤이니